Блог про инвестированиеДанный курс по основам статистике. Прочитав статьи, вы научитесь ориентироваться в величинах и статистическом анализе.
Подробный и понятный сбор статей.
Мы расскажем про сбор, обработку и анализ.
Известную фразу никто не отменял: есть лож, наглая ложь и статистика.
Но, я надеюсь вы будите применять свои знания не для подтасовок, а для объективного анализа. Статистический анализ помогает при принятии инвестиционных или управленческих решений.
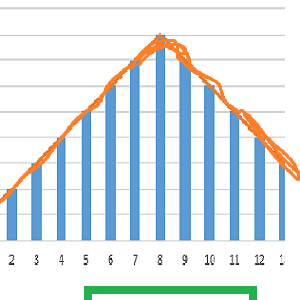
В теме вариационного распределения возникает вопрос как построить гистограмму. Да, кривую мы можем легко нарисовать по точкам (значениям) и получить что-то нечто похожее на нормальное распределение. Но, если нам нужна гистограмма, то сколько столбцов должно быть в ней. Определить количество столбцов в гистограмме можно простым методом – взять корень из N (количество значений). Но, лучше всего применить формулу Стерджесса.
(4 оценок, среднее: 3,50 из 5)
Загрузка...Стандартное отклонение позволяет описывать изменчивость наших данных. В статистике есть соотношения отклонений, когда они прибавляются и вычитаются к средниму (S, 2S, 3S). Если одно стандартное отклонение (Сигма), то вероятность 68,3%. Плюс-минус 2S вероятность 95,5%. И при интервале плюс-минус три сигмы дает 99,7%. Для нормального распределения чем больше отклонение, тем больше вероятность. В данной статье рассмотрим стандартное отклонение: график и особенности.
(1 оценок, среднее: 5,00 из 5) Загрузка...В статистике любят нормальное распределение. Основные методы в науке применяют данный закон. Строить оно по гистограмме. Упорядочиваем от минимума к максимуму. Разбивается распределение по интервалам. Мы рассмотрим свойства закона нормального распределения.
(1 оценок, среднее: 5,00 из 5) Загрузка...Понять насколько сильный разброс и степень отклонения всех значений от среднего нам поможет дисперсия.
(1 оценок, среднее: 5,00 из 5) Загрузка...Если мы говорим, как наши данные располагаться по шкале. По мимо медианы (середины), есть и другие. То есть, медиана делит на две половины. А почему бы не поделить распределение на четыре отрезка или на пять.
(2 оценок, среднее: 5,00 из 5) Загрузка...И так вы уже знаете про разные типы величин. В этом уроке мы поговорим про вариационный ряд, моду и медиану. Отдельно про медианы и моду подробно опишем.
(1 оценок, среднее: 5,00 из 5) Загрузка...Следующее, о чем мы с вами поговорим. Средние величины позволяют обобщить количественные данные. Бывают разные виды средних величин: арифметическая (простая или взвешенная), геометрическая, гармоническая (простая или взвешенная). Давайте рассмотрим каждую.
(1 оценок, среднее: 5,00 из 5) Загрузка...
Что представляют собой абсолютные и относительные величины мы скажем немного позже. Для начала поясним про совокупность. Существует генеральная совокупность – это все. Все кто есть номинально. Допустим все женщины, которые живут в городе Москве. Но, мы же не будет опрашивать всех женщин по всей Москве. Нам достаточно, опросить пару десятков, чтобы сделать вывод по всей совокупности (всем).
(1 оценок, среднее: 5,00 из 5) Загрузка...