Понять насколько сильный разброс и степень отклонения всех значений от среднего нам поможет дисперсия.
Вот пред вами точки — это индивидуальные значения и средняя в виде линии.
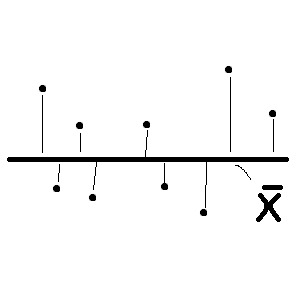
Чем меньше разброс, тем точнее выборка. В нашей совокупности находим среднее значение. Сравниваем каждый показатель Xi со средним значением Xср. Потом это все суммируем и делим на количество n.
Дисперсия — это оценка разброса всех показателей от среднего. Мы смотрим степень отклонения, насколько далеко показатели отходят от среднего.
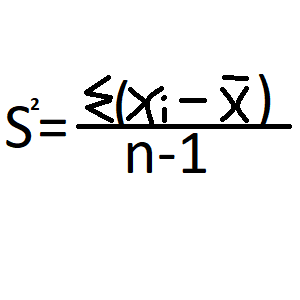
Вычисляем разность каждого показателя со средним значением. Суммируем эти значения, далее делим на количество показателей. Но, тут, две ситуаций. При определении дисперсии в генеральной совокупности мы делим данную сумму на n. А вот, при вычислениях дисперсии в выборке, делим уже n-1.
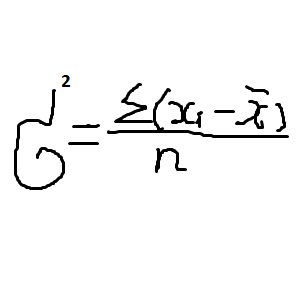
Конечно, в итоге мы находим СКО (среднеквадратическое отклонение) — S. А если работаем с генеральной совокупностью, то ищем Сигму. Тоже самое, что и дисперсия только в корне.
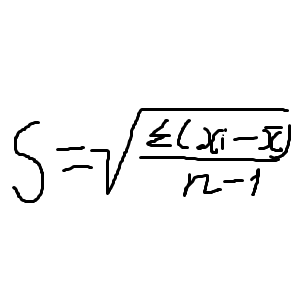
Стоит уточнить, мы все делаем в условиях нормального распределения. Про такое распределение мы поговорим в следящей записи.
(1 оценок, среднее: 5,00 из 5)
Загрузка...