В статистике любят нормальное распределение. Основные методы в науке применяют данный закон. Строить оно по гистограмме. Упорядочиваем от минимума к максимуму. Разбивается распределение по интервалам. Мы рассмотрим свойства закона нормального распределения.
Основная плотность в середине. А минимальные и максимальные значения принадлежат небольшому количеству признаков. Например, 90% умных, 5% мудрых и 5% глупых.
Кстати, в теорий управления любят это свойство. Объект управления оказывает воздействие на объект с ожиданием того, что 90% будет реагировать нужным образом, 5% не будет подчиняться и 5% очень активно проявят себя.
Считается, что если мода, медиана и средняя блики друг к другу по значениям, то это нормальное распределение.
Это не критерий!
В зависимость от того какое отклонение (СКО), распределение может иметь разные вид кривой. Тут, важно заметить, что для выборки мы используем среднюю, а вот для генеральной совокупности математическое ожидание Ню.
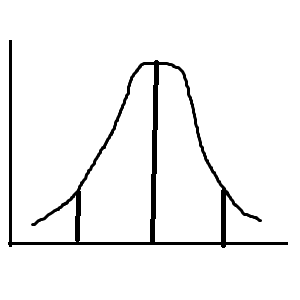
Когда исследование не подчиняться закону нормального распределения их называют непараметрическим. Как проверить на нормальное распределение? Графически – по виду, но это несерьезно. Сравнить моду и медиану тоже можно, тоже поможет предположить. Но, нужно вычислить по критерию нормального распределения или проверить гипотезы.
В целом, такие свойства закона нормального распределения говорят нам об этом.
Я обычно кривую распределения разбиваю на квартили.
(1 оценок, среднее: 5,00 из 5)
Загрузка...